A key enabling element for the realization of cooperative multi-agent missions is the availability of efficient cooperative motion planning strategies that can be implemented onboard the vehicles. A planning algorithm has to work within a complex set of constraints, and (near) real-time generation of trajectories is desired to allow the vehicles to re-plan their trajectories, if necessary. Typically UAVs carry low power-consumption processors with limited memory in order to save weight for maximum payload and flight endurance capabilities. Therefore, the planning algorithm has to be computationally efficient. It is in this spirit that our research group works toward the development of trajectory generation methods that allows for efficiently generating trajectories for multiple cooperating vehicles. A typical scenario is depicted in Figure 1, where three fixed-wing UAVs need to arrive at their final destinations while satisfying inter-vehicles safety constraints, vehicles’ dynamic constraints, and mission specific constraints such as simultaneous time of arrival.Our work is based on the use of Bezier curves, defined by Bernstein polynomials, which have favorable geometric and mathematical properties. We formulate the cooperative trajectory generation problem as a continuous-time optimal control problem, and approximate it by a discrete-time formulation using Bernstein polynomials. These polynomials allow for efficient computation of constraints (e.g. minimum distance between trajectories, input saturation constraints, etc.) along the whole trajectory, and are particularly convenient for generating optimal trajectories for safe operation of multiple vehicles in complex environments. The benefits of using Bezier curves for trajectory generation in multi-agent missions are discussed in [1] and [2]. Reference [2] uses Bezier curves to address the problem of distributed trajectory generation for a large fleet of agents. Finally, reference [3] analyzes the convergence properties of the proposed framework and presents a comparison with other techniques based on direct methods.

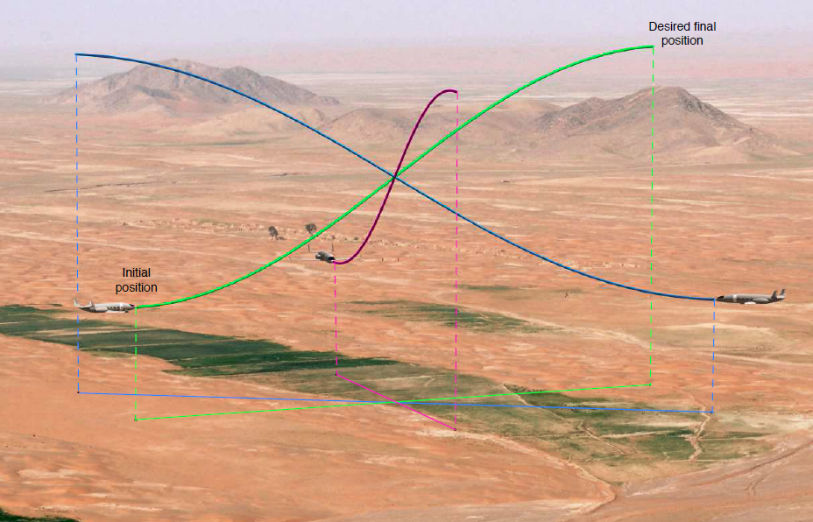
Figure 1. A typical scenario of cooperative trajectory generation