Time-Critical Cooperative Path Following
The objective of this work is to develop, implement, and test robust decentralized strategies for path-following control and time-coordination of a fleet of multiple autonomous vehicles supported by an inter-vehicle dynamic communications network. The methodology for time-critical cooperative path-following control developed at the ACRL (in collaboration with NPS and IST) can be summarized in three basic steps:
- Initially, each vehicle is assigned a feasible path with a desired speed profile that together satisfy the mission requirements, the vehicle dynamic constraints, and the optimal temporal specifications for each of the vehicles, while ensuring collision-free maneuvers.
- Then, a path-following algorithm ensures that every vehicle follows its own path independently of the temporal assignments of the mission.
- Finally, the vehicles coordinate their position along the path with the remaining vehicles engaged in the mission by exchanging coordination information over the supporting communications network. The different members in the fleet are classified per their behavior and informational needs as shown in Figure 1:
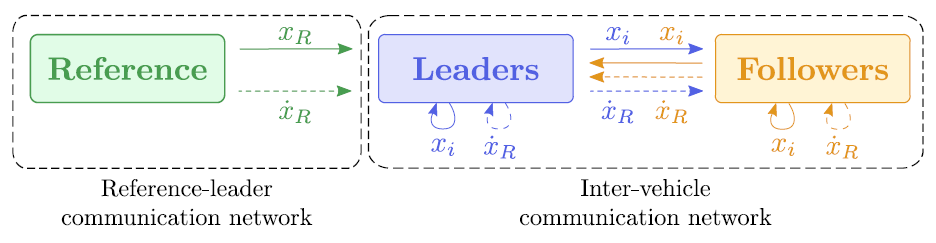
Figure 1: Communication networks, vehicle hierarchy, and flow of information
b) Leaders have direct access to the data from the reference agent, and communicate with other leaders and followers. In fact, leaders exchange their coordination states with other vehicles to achieve coordination.
c) Followers do not have direct communication capabilities with the reference agent. However, each follower shares its coordination state with other followers and leaders.
Additionally, to increase the usability and applicability of the time-coordination algorithm this project seeks to widen the spectrum of coordination and temporal constraints that can be imposed on the fleet, summarized in Figure 2:
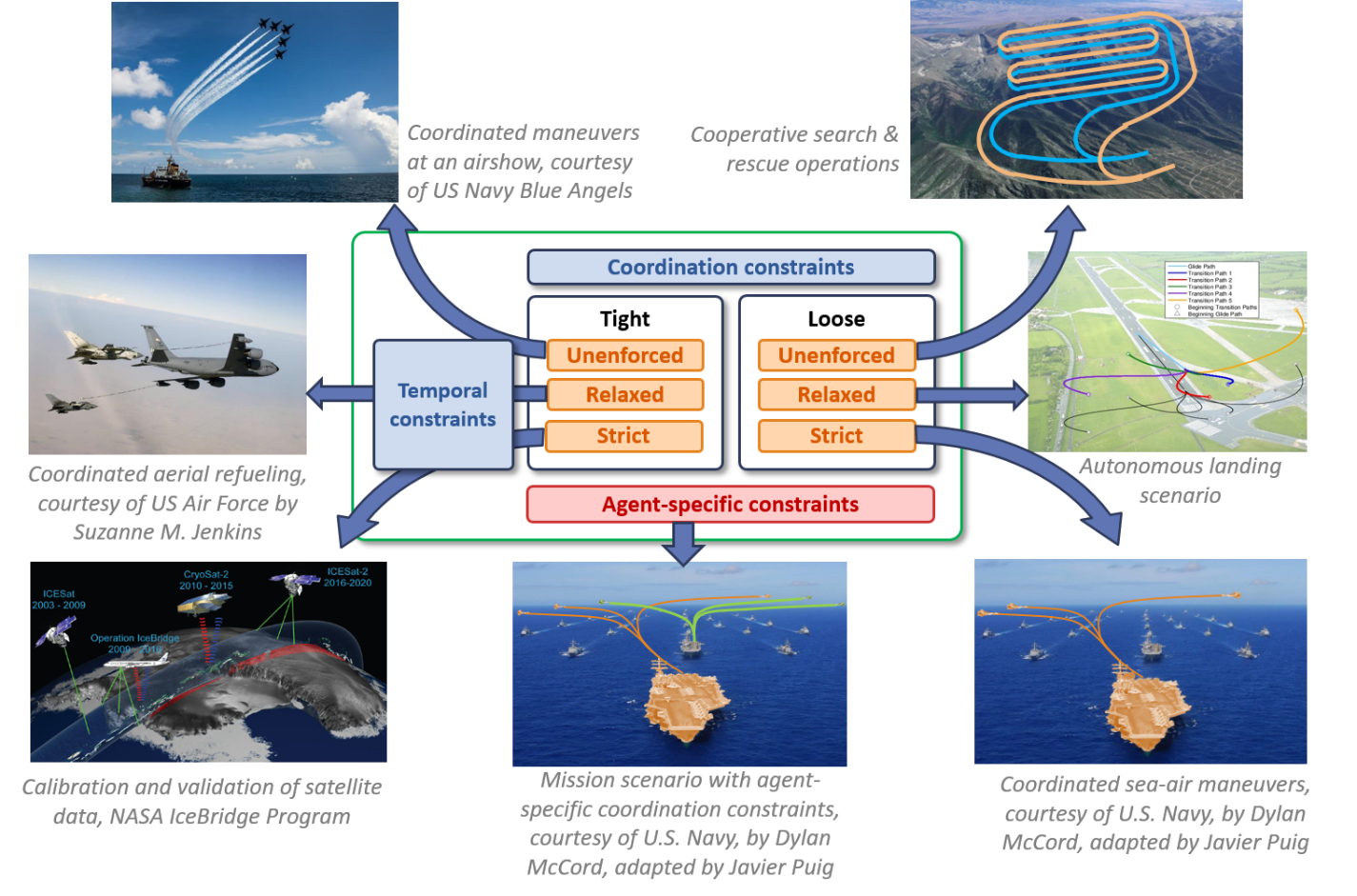
Figure 2: A variety of time-coordination constraints considered
The three fundamental steps are accomplished by judiciously decoupling space and time in the formulation of the trajectory-generation, path-following, and time-coordination problems. Moreover, the approach adopted applies to teams of heterogeneous vehicles and does not necessarily lead to swarming behavior, which is unsuitable for some of the mission scenarios envisioned in this project.
Some earlier results have been implemented on Fixed Wing and Quadrotor UAVs.
References
- J. Puig-Navarro, N. Hovakimyan, and B. D. Allen. Time-coordination strategies and control laws for multi-agent unmanned systems. In Proceedings of 17th AIAA Aviation Technology, Integration, and Operations Conference, 2017.
- J. Puig-Navarro, E. Xargay, R. Choe, and N. Hovakimyan. Time-critical coordination of multiple UAVs with absolute temporal constraints. In Proceedings of AIAA Guidance, Navigation and Control Conference, 2015.
- E. Xargay. Time-critical cooperative path-following control of multiple unmanned aerial vehicles. PHD Thesis, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 2013. (link to this thesis)
- E. Xargay, I. Kaminer, A. Pascoal, N. Hovakimyan, V. Dobrokhodov, V. Cichella, P. Aguiar, and R. Ghabcheloo. Time-critical cooperative path following of multiple UAVs over time-varying networks. In Journal of Guidance, Control, and Dynamics, Vol. 36, No. 2, 2013.
- E. Xargay, V. Dobrokhodov, I. Kaminer, A. Pascoal, N. Hovakimyan, and C. Cao. Time-critical cooperative control for multiple autonomous vehicles. In IEEE Control Systems Magazine, Vol: 32, Issue: 5, 2012.
- V. Cichella, I. Kaminer, E. Xargay, V. Dobrokhodov, N. Hovakimyan, P. Aguiar, and A. Pascoal. A Lyapunov-based approach for time-coordinated 3D path-following of multiple quadrotors in SO(3). In Proceedings of 51st IEEE Conference on Decision and Control (CDC), 2012.